Editorial
Reconsideration of Gerstmann’s Syndrome in the Lights of Current Knowledge Sand Spaces of Irrational Numbers
Aydin MD*
Department Neurosurgery, Medical Faculty of Ataturk University, Turkey
*Corresponding author: Aydin MD, Department Neurosurgery, Medical Faculty of Ataturk University, Erzurum, Turkey
Published: 29 Nov, 2017
Cite this article as: Aydin MD. Reconsideration of
Gerstmann’s Syndrome in the Lights
of Current Knowledge Sand Spaces of
Irrational Numbers. Clin Surg. 2017; 2:
1768.
Gerstmann’s Syndrome
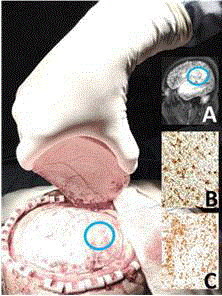
The disorder was first described by Dr. Josef Gerstmann, a Viennese neurologist, in 1924. Gerstmann syndrome is a rare neurological disorder that can occur as the result of a brain injury or as a developmental disorder. Thes syndrome is characterized by a graphia/dysgraphia, acalculia, finger agnosia and toun distinguish between the right and left sides of one's body. The cause of Gerstmann syndrome is various damages of the upper side of parietallobes. Gerstmann syndrome affects males and females in equal numbers. Gerstmann’s syndrome is seen in patients with various focal lesions situated subcortically in the left angular gyrus. Functional MRI studies shows any lesion localized to the dominant superior parietal lobe and the dorsal aspects of the inferior parietal cortex [1], insularor peri-insularlesion [2]. Tumors, cysts, traumas, infections, intoxications, metabolic diseases an congenital pathologies may be responsible for Gerstmann’ssyndrome. Diagnosis is proven by routinely radiological technics and noenough treatment way [3]. Angulary gyrus localisation is seenbase; MRI appearances of a patients with Gerstmann’s syndorome (A), normal glio-cyto architectures of angularygyrus (B) and glial cells in a glial tumor detected patient with Gerstmann’s syndrome developed patient (C) is seen in (Fıgure 1).
Acknowledgements on Mathematical Abilityand Brain
The development of math skills is a critical component of early education and a strong indicator of later school and economic success. Recent math achievement suggest that structural and functional integrity of parietal regions, especially the angulary gyrus, and increased gray mattervolume in the bilateralhippo campalformationand the right inferior frontal gyrusare closely related to the development of mathskills [1,2]. Angulary gyrus discovered simple numbers and solves simple mathematical problems; but, it has not known irrational numbers and related problems yet!. Ifso, angularg yrus has not been thoroughly developed tounder stand irrational numbers.
What are Irrational Numbers?
An irrational number is a number that cannot be expressed as a fraction p/q forany integers p and q. Irrational numbers have decimal expansions that neither terminate nor be come periodic. Every transcendental number is irrational. Irrational numbers may not be crazy, but they do sometimes bend our minds a little.
A- √2 (1,414213….)
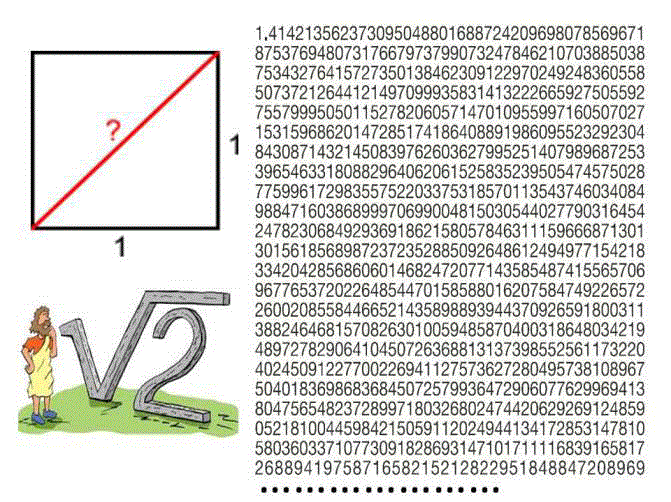
The most famous irrational number is √2, sometimes called Pythagoras'sconstant. Other examples include √3, e (Euler number), π (Pi), Φ (Golden ratio)etc. Don't assume that irrational numbers have no thing to do with madness. Around 500 B.C.,when Hippasus demonstrated the irrationality of √2, he was immediately thrown overboard by the fanatic Pythagoreans, a group of Greek. It's a stormy day on the seaoff the coast of Greece. The date is around 520 BC., fighting for his life, a man is heaved overthe side of a boat and Hippasus dropped into the open water todie. What is His crime? Telling the world a mathematical secret of the dangerousratio.The murder of Hippasus should be done according to Pythagoreans, because the secret deleted the faith of Pythagorean religion, and certainly dangerous enough to the beliefs of those who knew about it. It was a secret owned by the school of Pythagoras. All early greek mathematicians were obsessed with the significance of whole numbers and their ratios. The Pythagorean's believed that "All is number" and the universe was built around the whole numbers. ‘’Each number from one to ten was given a very special significance. Odd numbers were thought to be male and even numbers female’’. Yet there was one number that the Pythagoreans found dangerous, the number that might have cost Hippasus’ life for revealing its existence of square root of two to the world. Pythagoras is the best remembered for a geometrical theorem, the one that tells us how to calculate the lengths of the sides of a right angled triangle, and it is from this theorem that the dangerous ratio emerges. Imagine a simple square shape, each side 1 unit in length. How long is the square's diagonal? [4]. (Figure 2) shows of calculation method and values of square root 2; and a memorial drawning to represent of Hippasus’sstatus in historical perspectives.
Figure 1
Figure 1
Angulary gyrus localisation is seen base; MRI appearances of a
patients with Gerstmann’s syndorome (A), normal glio-cyto architectures
of angulary gyrus (B) andglial cells in a glial tumor detected patient with
Gerstmann’s syndrome developed patient (C).
B- π: (π = 3.141592...)
The circumference of a circle divided by its diameter is always a little more than 3Infact, the result of this division is an irrational number that we commonly refer to as π. π is part of a group of special irrational numbers that are sometimes called transcendental numbers. These numbers cannot be written as roots, like the squareroot of 11. As of 2011, people have discovered more than 5 trillion digits of π, but we'll never get to the end of it, because there is no end! Sometimes you might see pi written as 22/7; however, be aware that, like 3.14, 22/7 is only an approximation. It is close to π, but it's not equal. There is no fraction that exactly equals π.
C- e (Euler's Number): (2.7182818284...)
To mathematicians, e is more than just a letter in the alphabet the irrational number e is formally named Napier's constant, but it is commonly called Euler's number, after LeonhardEuler (pronounced 'Oiler'). Justlike pi, e occurscommonly in therealworld.
D- Φ (Golden ratio): (1.61803399…)
Is there a number it is interesting all humankind. This “golden” number, 1.61803399, represented by the Greek letter Phi, is known as the Golden Ratio, was written about by Euclid in “Elements” around 300 B.C., by Luca Pacioli, a contemporary of Leonardo Da Vinci, in “De Divina Proportione” in 1509, by Johannes Kepler around 1600 and by Dan Brown in 2003 in his bestselling novel, “The Da Vinci Code.” ‘’The Fascination of “The Da Vinci Code” was that it creatively integrated fiction with both fact and myth from art, history, theology and mathematics which reader never really known what was truth and what was not. Its mathematical cousin, the Fibonacci sequence (0, 1, 1, 2, 3, 5, 8 …). Both of which have roles in the plot of this murder mystery, and distinguishes between the myth and the math [5].
Figure 2
Figure 2
Calculation method and values of square root 2; and a memorial
drawing to represent of Hippasus’s status in historical perspectives. Nagell
T, Introduction to number theory. New York: Wiley, pp. 38-40, 1951; Brian
Clegg: The Dangerous Ratio. February 2011.
A Brief Summary on the Failure of Angulary Gyrus
If the development of math skills is a critical component of the brain; and structural and functional integrity of the angulary gyrus to gether with graymatter volume in the bilateral hippocampal formation and the right inferior frontal gyrus are closely related to the development of math skills; why the angularygyrus has not known irrational numbers and related problems yet!.If so, angulargyrus has not been thoroughly developed to understand irrational numbers? According to that theories, all of us have Gerstmann’s Syndrome?
References
- Bhattacharyya S, Cai X, Klein JP. Dyscalculia, dysgraphia, andleft-rightconfusionfrom a leftposterior peri-insularinfarct. BehavNeurol. 2014;2014:823591.
- Wu YT, Chen LC, Lin SL, Chang ST. Gerstmann's syndrome associated with diagnostic cerebralangiography. Brain Inj. 2013;27(2):239-41.
- Aydin MD, Aydin N. A Cerebral Hydatid Cyst Case First Presenting with GerstmannsSyndrome: A Case Report and Literature Review. Turk J Med Sci. 2003;33:57-60
- Apéry, R. Irrationalité de et. Astérisque. 1979;61:11-3.
- Bailey D H. Crandall RE. Randomgeneratorsand normal numbers. Exper. Math. 2002;11(4):527-46.
- Hardy GH. Wright EM. An ıntroduction to the theory of numbers. 5th ed. Oxford: England: Clarendon Press; 1979.
- Nagell T. Irrational numbers and ırrationality of the numbers and. §12-13 in Introduction to Number Theory. New York: Wiley. 1951;38-40.
- Niven, I. M. Irrational numbers. New York: J. Weley; 1956.
- Pappas T. Irrational numbers the pythagoras theorem. The joy of mathematics. San Carlos, CA: Wide World Publ./Tetra. 1989;98-9.
- Brian Clegg. The Dangerous ratio published november 2004.
- Wilkey ED, Cutting LE, Price GR.Neuroanatomical correlates of performance in a state-wide test of mathachievement. Dev Sci. 2017.
- GaryMeisner. GoldenRatioOverview. 2015.