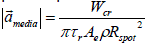Research Article
Identical Geometrical Profile for both Craters and Arbitrary Long Incisions Produced by CO2 Laser Beams onto Irradiated Biological and Non-Biological Samples: The Acceleration of the Lesion’s Horizon is a Fundamental Growth Indicator for any CO2 Laser Ablation and it is Confirmed by Two Independent Analytical Approaches used Across Both Samples Families
Franco Canestri*
University of Tel Aviv, Israel
*Corresponding author: Franco Canestri, Research Fellow, University of Tel Aviv, Tel Aviv – Israel (1993-1994 and 2010) and National Cancer Institute, Milan – Italy
Published: 26 Apr, 2017
Cite this article as: Canestri F. Identical Geometrical
Profile for both Craters and Arbitrary
Long Incisions Produced by CO2 Laser
Beams onto Irradiated Biological
and Non-Biological Samples: The
Acceleration of the Lesion’s Horizon is
a Fundamental Growth Indicator for any
CO2 Laser Ablation and it is Confirmed
by Two Independent Analytical
Approaches used Across Both Samples
Families. Clin Surg. 2017; 2: 1434.
Abstract
In order to forecast with sufficient precision the geometrical profile of a cut obtained via a moving
surgical CO2 laser beam emitting in continuous wave (CW), it is recommendable to produce a single
crater with the same desired safety depth and acceptable superficial damage first. This precaution
allows to reduce the risks of starting an uncontrolled cutting process with unfavorable consequences:
a single crater allows to test the selected laser set-up (output power, focal length and beam profile)
under minimal damaging conditions in a volume with the same structural and thermodynamic
characteristics of the cut and where no significant irreversible and permanent large damages can
occur.
The next logical step is then to select a proper scanning speed of the same laser focal head and
modified set-up over the surgical area to treat, which then would allow producing a cut with the
identical safe profile obtained with the single accepted test crater (“crater-first-to-cut” approach).
In more mathematical terms, the incognita to determine is the correct power density distributed
over the complete desired cut length which produces the identical geometrical profile of the original
test crater. As consequence, the correct “cut – speed” equation must guarantee the production of
the original test crater profile all the way from the start to the end of the desired arbitrary incision.
This Paper presents two separate analytical models and proposes some preliminary experimental
results to be considered for both crater pre-testing and cut generation phases obtained via CW -
CO2 laser beams during forecasting and pre-simulations of challenging interventions in Operating
Room. The experimental evidence of the presence of an acceleration phase during the early crater
production process in both biological and non-biological is presented and discussed as well.
The reverse approach “cut-first-to-crater” will be discussed by the Author in a separate future Study.
Keywords: Crater; Incision; Cut; CO2 lasers; Continuous wave; PMMA; Power density; Speed;
Focal head; Biological media; Geometrical profile; Horizon; Radius; Depth
Introduction
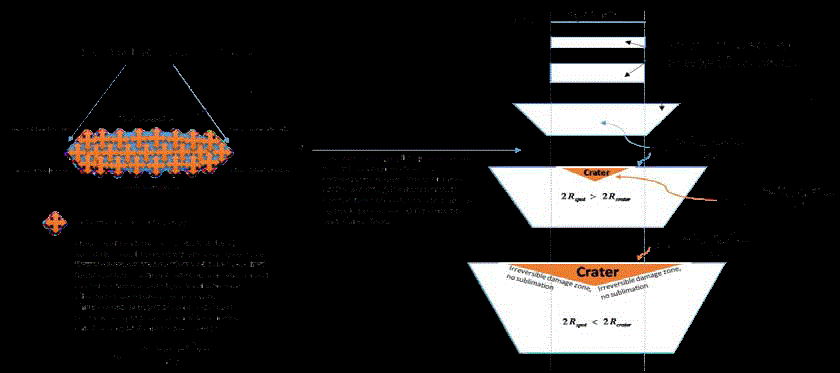
The CO2 laser is one of the highest-powered and most efficient lasers that are currently available, and is one of the most useful in very many medical and surgical applications since more than 40 years [1-3]. Laser surgery uses an intensely and precisely focused beam at 10.6 μm to remove or vaporize tissue while controlling the bleeding in a wide variety of non-invasive and minimally invasive procedures. However, the invasive aspects of the laser beam below the surface to be treated generate all sorts of safety questions concerning the uncontrolled and invisible spreading of the beam near delicate vital organs while treating the volume of interest. A less invasive single crater on the mass to be treated simulates acceptable limiting geometrical boundaries and it can therefore be used as safety reference margin for more complex and challenging longer incisions near vital organs. These ones must be protected during any surgical procedures when CO2 lasers are in use.
Table 1
Table 1
Irradiated Non-biological Media (PMMA) - all data in CGS Unit System. In yellow, samples with peculiarities.
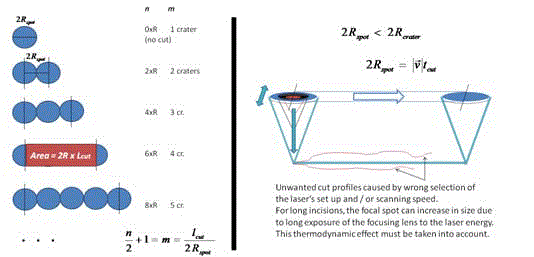
Preliminary data on minimal incision length (m = 2). For all samples : Vspot tcut = 2mRspot.
Table 2
Table 2
Irradiated Biological Media - all data in CGS Unit System. In yellow, samples with peculiarities. Preliminary data on minimal incision length (m = 2). For all
samples : Vspot tcut = 2mRspot.
Materials and Methods
A commercial TEM00 - CO2 laser has been coupled to regular
focusing heads to be used for continuous wave (CW) laser beam
delivery trials on in-vitro biological and non-biological samples. The
TEM00 mode stands for “Gaussian Transversal Electromagnetic
Mode” of the beam. Several experiments have been conducted (Table
1 and 2) using particular combinations of laser optical parameters in
output, depending on each case-by-case need. The total exposure time
was kept to 10 sec. for the entire set of experiments. Several samples of
the same tissue type have been irradiated under the same laser output
conditions and all with the laser beam perpendicular to the surface
and at the laser spot. All the irradiated samples have been considered
for the final calculations and the resulting damage measurements.
Five rabbits weighting 3 to 3.5 kilos have been sacrificed and 60
samples of trachea, myocardium, aorta and esophagus have been
immediately excised, separated free of the adherent connective tissue
and irradiated in the intima portion of the wall. The exposure distance
above the surface to be irradiated was kept identical to the focal length
of the lens in use. Each sample was examined in the fresh state and
after the exposure to the laser irradiation for gross evidence of tissue
charring black carbonized spots and craters. After irradiation all the
in-vitro samples have been fixated immediately in buffered formalin
for 72 h, cleared with xylene, impregnated and embedded in paraffin
and cut at 6 μm intervals. Each section was stained with hematoxyline/
eozine and examined via optical microscopy. The slides were
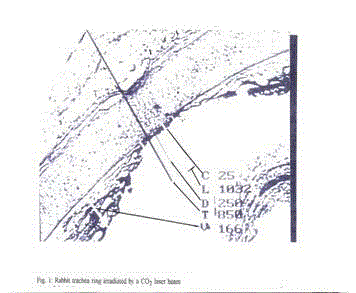
computer analyzed to measure the dimensions of the lesions, marked
with ‘2R’ for the diameter and ‘Z’ for the depth and photographed
(Table 1 and 2). As control group, 10 plastic blocks (1 cm × 3 cm ×
3 cm) have been irradiated with the same optical focusing heads in
order to obtain clearer crater structures to allow better observation,
more precise dimensional measurements and clearer comparison
(Figure 1 and 2). These plastics chemically belong to the families
of the polymethil-methacrylates (PMMA). Also, these experiments
have been conducted to simulate the responses to the laser radiation of hard, low-water content tissues such as bone [3-5]. Also, these
plastics are routinely used in orthopedic surgery as bone cement to
repair severe fractures [5]. All the ‘injury diameters 2R’ and ‘injury
depths Z’ reported in Table 1 and 2 are averaged over the number
or experiments per type of tissue. Their tolerances are reported in %
in Table 1 and 2 for all the samples and tests, including the PMMA
ones. The PMMA samples show a compact and transparent hard
structure [6] which allows very precise geometrical measurements.
In order to have a third control group for comparison, additional
measurements with two focusing heads 2.5“ and 5“ focal lengths
have been conducted. These measurements have been obtained by
irradiating each sample perpendicularly and on the spot of each used
focal. The spot sizes are : 0.2 cm diameter of the spot produced by the
8.7” focal in TEM22 mode, 0.01242 cm diameter for the 2.5“ focal and
0.02484 cm for the 5“ focal, both for TEM00 Gaussian mode. Only
the three types of plastics have been used at 2.5” and 5” focal: due to
the high power density on the beam spot caused by these two specific
focal lengths, this decision was necessary not to cause too destructive
thermodynamic damages on the biological sample.
Discussion about the two models: A) the speed- versus B)
the global-based approaches
A) The fundamental starting consideration is to
make sure that the same laser beam power density
Imax (Watt/spot area = Joules/time × spot area) for both single
crater and cut generation procedures gets delivered on the surface
to be treated in order to create the same safety sublimated profile in
both circumstances. Two additional assumptions are: the spot area is
circular and the scanning speed /v/ of the focusing head is constant.
Based on this, the key mathematical equations to consider are:

The basic condition to respect in order to achieve the same geometrical
“diameter – depth” profile for both single crater and arbitrary cut is
to deliver the same power density I0 (W / cm2) on the same laser spot
size.
The laser can have different focal lengths fx, different wavelength
λ and different beam profiles (TEM = Transverse Electromagnetic
Mode), therefore the power density for both crater and cut generation
procedures can be written from Eq. (1) and (2) as follows:
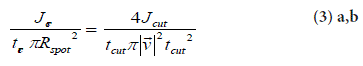
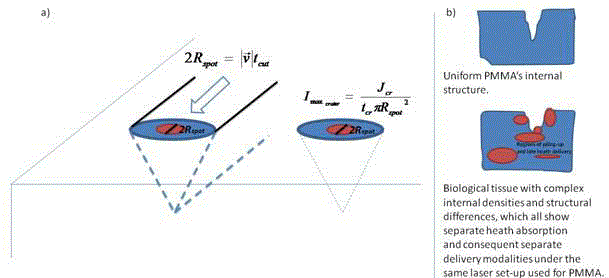
where the diameter of the spot size for a CO2 laser beam is:
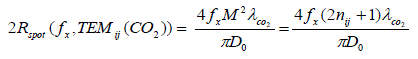
where J is the selectable output energy in Joules, Rspot is the spot
of the focal in-use and /v / the scanning speed of the focusing head
transiting over the surgical area. D0 is the diameter of the laser beam
before passing through the focusing lens of the laser focusing head
(data provided by the Laser Manufacturer) while the numerical factor
‘n’ is the number of modes of beam in use: for a large TEM laser
beams, n=5 has been used while for the TEM00 Gaussian mode we
must use n=0 at all times [7,8].
Moreover tcr is the total exposure time on a single 2Rspotdiameter
spot, tcut is the time required to pass over any arbitrary
2Rspot-diameter-long section contained in the total cut length to be
produced, Jcr is the total energy in Joules delivered over the spot and
Jcut is the total energy delivered by the moving focusing head while
scanning any arbitrary 2Rspot-diameter-long section of the total cut
(Figure 1) in order to obtain the same geometrical profile of the single
crater.
From Eq. (3a), the required Jcut as function of the scanning speed
is:

As shown in Figure 3, the heath conduction modalities on the
crater and on the cut are completely different, meaning that small
parts of energy are gradually but rapidly taken away from the surface
of interest while the focusing head is transiting over the surface.
These small quantities do not contribute to the generation of the
crater: therefore, in order to achieve the same geometrical profile, the
energy delivered on the cut must be higher than the one need for the
single reference crater [9]. Here, the heath conduction is stable and
therefore the remaining energy in Joules is piling-up to the quantity
needed to create the reference crater profile to be used later for the
cut production.
This means from Eq. (4):

Another important consideration must be considered now.
The vertical acceleration [10] of the crater development along the Z
coordinate (crater depth – Table 1 and 2) can be used to define the
upper limit of the required exposure time for the cut development
process.
Therefore from Eq. (4) and Eq. (5), all these considerations lead
to:
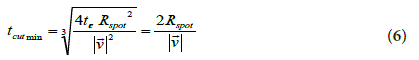
while the boundary conditions given by the experimental results on the selected media can be considered this way (uniformly accelerated motion model):
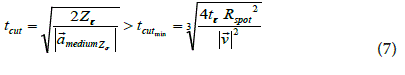
This is needed in order to allow Jcut > Jcrater, as described in Eq. (5) and in Figure 4. Here, the peak vertical acceleration [10] of the crater for the irradiated media is:
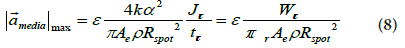
Assuming that the acceleration of the crater depth production is
constant (Table 1 and 2).
ε, α, ρ, α, ρ, τρ, k k and Ae are all thermodynamic parameters
described with greater details by the Author is several Publications
already [10,11], including the fact that ε=1 along the Z coordinate
and in the range of 0.5-0.8 for the X,Y ones [11]. By using the
experimental results presented in this Paper, the correct value is 0.55
+/- 10% for non-biological media (PMMA) but no precise limit can
be given for the biological ones, where the inherent bio-chemical
characteristics of each sample are very dependent on the structure of
the irradiated one. This fact is related to the large uncertainty amongst
the resulting acceleration values measured on different samples.
The theoretical value presented by the Author in [10,11] is equal to
0.88 for the PMMA.
We can define the following numerical parameter as follows
(Figure 5a):

Now, both cut and crater have the same profile if the power density is the same:
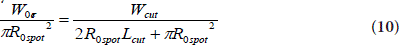
Where “0” indicates the known magnitudes (a-priori selected or
calculated by the user).
By using Eq. (9) we can easily calculate:
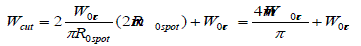
This allows us to find via Eq. (4) the relationship valid for any 2Rspot -crater along the cut:
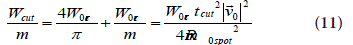
The two unknown’s tcut and the acceleration ‘a’ can be obtained via the following system:
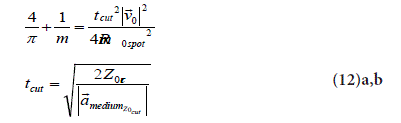
The suffix “cut” for the acceleration is now needed in order to underline the parallelism (Figure 5 and 6) “crater – cut” for the same desired crater-cut profile onto the selected media:
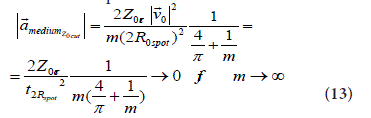
For m ◊ 1, the following single crater’s horizon acceleration (at Z0) can be expected:
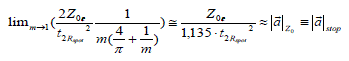
This approximation must be validated with more precision for
PMMA vs. biological media.
B) In order to further analyze the cut development along its
length L in a more global manner and then compare the results from
both approaches, we can say that both power densities after the crater
and after the cut (m=2) production must be equal:
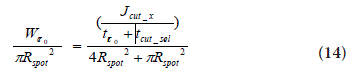
The case here reported simulates the basic reference cut obtained
with m=1. The unknown is Jcut x and it has to be equal to the one
calculated via Eq. (4). Without any corrective measures, each single
systematic error on Jcut (for the entire set of experiments (Table 1 and
2) between Eq. (4) and Eq. (14) is less than 0.5%: a very small and
constant value that points out to the same representation of the all
experimental conditions (Table 1 and 2).
If the sweeping time over the spot arbitrary changes, then
the power density on the spot changes as well, causing complex
cross-modifications in all the equations reported above and
ultimately resulting in the wrong generated cut profile (Figure
6). In-fact, the outcomes of Equations (1) to (13) have to be
considered related only to one selected laser set-up: therefore,
a new laser set-up generates its own new and different set of data.
Consequently and logically, only one acceleration value of the crater
horizon must then correspond to each selected laser set-up itself.
Instead, from Eq. (13) there are two of them:
i) One obtained for m=2, which means “shortest possible cut=2
x crater”, following
Eq. (2) in order to have an absolute initial speed reference, and
ii) The other one obtained for m ◊ 00, which means “longest
possible cut”.
The numerical difference between the two is large, in contrast to
the fact that there must be only one referenced to the shortest possible
cut (1 x crater, case a)). The reason is that Equation (13) does not
take into consideration that “very long cut” correspond to “very long
beam exposure” of the laser lens to the beam, meaning that larger
and larger heath quantities are absorbed by the lens itself. This results
into non-linear geometrical modifications of the it (see both fx and
(2nij + 1) in Eq. (3) b), causing therefore an enlargement of its focal
spot for the same beam aperture D0. The same output energy on a
larger and larger focal spot (lower and lower power density) reduces
the penetration capability of the beam itself, causing therefore
a lower and lower vertical acceleration of the crater’s horizon.
Following these considerations, the presence of acceleration has been
experimentally demonstrated in the present Study and the different
behavior of the accelerated crater growth across several different
irradiated media has been confirmed as well.
For all the cases reported in Table 1 and 2, the following
relationship for m=2 are satisfied:
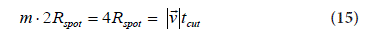
More investigations are needed to confirm all these conclusions with stronger evidence on a larger set of biological media and for longer cuts with m >> 2, therefore with Lcut >> 2Rspot. In case of any arbitrary speed of the focusing head, then the comparison to a single safe crater as initial starting reference point cannot be used any longer (this Study). This different “cut-first-tocrater” approach (based on Eq. 10 as starting point) requires additional separate investigations which will be presented and discussed by the Author in the near future.
Figure 1
Figure 2
Figure 3
Figure 3
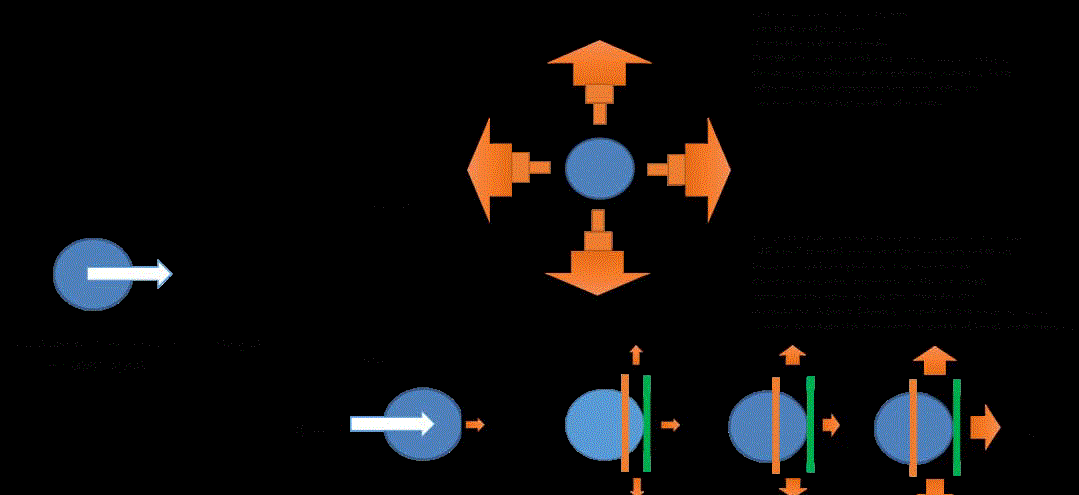
Heath conduction modalities (red arrows) between scanning (cut) and fixed (crater) focusing head on the spot. The heath quantities conducted away
from the target do not contribute to the sublimated crater profile. During the formation of the crater, the conducted heath increases over the same geometry, not
like in the cut mode.
Figure 4
Figure 5 a,b
Figure 6
Figure 6
Three dimentional rendering of craters versus cuts, depending (b)) on biological or non-biological tissue characteristics. For very long incisions, the lens
geometry can vary, meaning that the spot size increases due to long exposure to heath.
Discussion
This Paper presents a comprehensive workflow which can
be summarized in the following way: when the laser beams focal
spot starts to scan the surface to be treated at a constant speed
“v”, then the output energy must be enhanced from “Jcr” to “Jcut”
within the time slot of max. “tcut” seconds. This will produce a cut
with the same geometrical profile of the crater previously obtained
during “tcr” and with “Jcr” into the same media and with the same
optical set-up. It is interesting to observe (Table 2) that the starting
acceleration along the Z coordinates in PMMA samples is larger
than the one at the bottom of the crater or cut: in biological tissue
the opposite happens, although over a very limited geometrical
range. The constant polymeric structure of the PMMA allows an
uniform accumulation of heath and consequent smooth ablation
also due to its low water content. On the contrary, the higher fluids
content of complex biological tissues requires longer initial time for
the transition to boiling and evaporation first, then to carbonization
and finally to ablation, leading to an increase of acceleration of the
energy piled-up energy and its consequent avalanche effect once the
ablative phase has become steady during “beam on”. Fat, liquids, hard
tissues and muscles accumulate energy differently and without any
thermodynamic changes until a critical limit is reached, causing a
sudden punctual “explosion-like” heath delivery along both vertical,
diagonal and horizontal directions (Figure 5b) [12-15].
In other words, the polymers start to ablate
very quickly and to dissipate heath uniformly
during irradiation also. The biological tissues instead cumulate energy
for a certain period of time until the first ablation takes place, then a
sort of explosion follows, as demonstrated by the Author in [16] as
well. The process then continues by releasing all the piled-up energy.
This phase corresponds to the increase of the acceleration of the crater
horizon, as here clearly demonstrated: for the same laser set-up, the
overall depth is smaller but growing at higher acceleration than in the
PMMA, which shows rather the opposite behavior. Now looking at
the other results reported in Table 1 and 2, similar power densities
on the spot generate very different Jcut requirements and associated
acceleration values, depending on the type of the biological media,
but mainly on the quantity of irradiated muscular and fat tissue [17].
On PMMA samples, very high power densities generate lower and
more uniform demand of Jcut, mainly due to its internal homogeneous
structure. For all the irradiated media under very different laser setups,
tcut oscillates in a very stable manner between 0.1 and 7.5 seconds
even considering the non-biological PMMA samples. Particular cases
have been marked in yellow on both Tables.
This procedure allows also to numerically quantify the crater
horizon’s acceleration: once more it demonstrates the existence of
this important parameter which was theoretically postulated by the
same Author in other previous studies [16,18]. Still, it is important
to mention again that the PMMA has a constant geometrical and
thermochemical structure and it can therefore generate equal
outcomes in Joules based on pure geometrical assumptions only.
More investigations are needed in order to further improve the
quality of this preliminary methodology and improve the consistency
of the results over very long incisions.
References
- Laufer G. Primary and secondary damage to biological tissue induced by laser radiation. Appl Opt. 1983;22(5):676-81.
- Clayman L, Fuller T, Beckman H. Healing of continuous-wave and rapid superpulsed, carbon dioxide, laser-induced bone defects. J Oral Surg. 1978;36(12):932-7.
- Canestri F. Proposal of a computerized algorithm for CW CO2 laser on-line control during orthopaedic surgery. Phase I: theoretical introduction and first in-vitro trials. Int J Clin Monit Comput. 1992;9(1):31-44.
- Canestri F. Proposal of a computerized algorithm for continuous wave CO2 laser on-line control during orthopedic surgery. Phase II: Simplified algorithm version (LCA-s) and helmet-mounted data access device solution. Int J Clin Monit Comput. 1997;14(3):199-206.
- Scholz C, Matthes M, Kar H, Boenick U. [Removal of bone cement with laser]. Biomed Tech (Berl). 1991;36(5):120-8.
- Canestri F. A proposed Clinical Application of a Model of CO2 Laser Radiation Induced Damage Craters. J Med Eng Technol. 1989;12(3):112-7.
- Johnston TF. Beam propagation (m(2)) measurement made as easy as it gets: the four-cuts method. Appl Opt. 1998;37(21):4840-50.
- ISO Standard 11146 “Lasers and laser-related equipment – Test methods for laser beam widths, divergence angles and beam propagation ratios”. 2005.
- Canestri F. Accurate quantification of the optical absorption coefficient and of the thermal relaxation time for PMMA and for low-water-content media during early ablation with CO2 laser beam at the wavelength of 10.6 μm. Photomed Laser Surg. 2011;29(1):61-6.
- Canestri, F. “Acceleration Bursts of the Crater’s Horizon at Each On-set of Pulsed CO2 Laser Ablation into PMMA Samples.” - ‘Lasers in Medicine’.2014;1(6).
- Canestri F. Ultra-Conservative Minimally Invasive Surgery (UCMIS) with Pulsed Non-Gaussian CO2 Laser Beams Focused Through the Shortest Possible Focal Length. Photomed Laser Surg. 2011;29 (11):759-66.
- Li Li, Mingchao Liang, Boming Yu, Shanshan Yang. Analysis of thermal conductivity in living biological tissue with vascular network and convection. Int J Thermal Sciences. 2014;86:219–26.
- Whiting P, Dowden JM, Kapadia PD, Davis MP. A One-Dimensional Mathematical Model of Laser Induced Thermal Ablation of Biological Tissue. Laser Med Sci. 1992;7(1):357-68.
- Kyunghan Kim, Zhixiong Guo. Thermal Relaxation Times in Biological Tissue Subjected to Pulsed Laser Irradiation. 2006;2938.
- Walsh JT Jr, Flotte TJ, Deutsch TF. Er:YAG laser ablation of tissue: effect of pulse duration and tissue type on thermal damage. Lasers Surg Med. 1989;9(4):314-26.
- Canestri F. Sudden and unpredictable below-surface ablation pattern changes by CO2 laser beams: a qualitative description of five macroscopic cases observed in PMMA with high probability to occur during surgery in low-water-content tissues. J Clin Laser Med Surg. 2002;20(6):335-9.
- Li ZZ, Reinisch L, Van de Merwe WP. Bone ablation with Er:YAG and CO2 laser: study of thermal and acoustic effects. Lasers Surg Med. 1992;12(1):79-85.
- Canestri F, Katzir A. “Pulsed CO2 laserbeam delivery and real time temperature Measurements.” - ‘SPIE Laser-Tissue Interaction Congress, Los Angeles,’ 1994; 2134A, Paper No. 477.