Research Article

On the use of Geometric Modeling to Predict Aortic Aneurysm Rupture

Sruthi L. Muluk^1*, Pallavi D. Muluk², Judy Shum³ and Ender A. Finol^4
1Harvard College, Cambridge MA, USA
²The Ellis School, Pittsburgh PA, USA
³The MathWorks, Natick MA, USA
⁴University of Texas at San Antonio, USA

^*Corresponding author: Sruthi L. Muluk, Harvard College, 294 Dunster Mail Ctr, 945 Memorial Drive, Cambridge, MA 02138-7544, USA

Published: 22 Dec, 2016
Cite this article as: Muluk SL, Muluk PD, Shum J, Finol EA. On the use of Geometric Modeling to Predict Aortic Aneurysm Rupture. Clin Surg. 2016; 1: 1252.

Abstract

Background: Currently, the risk of abdominal aortic aneurysm (AAA) rupture is determined using the maximal diameter (Dmax) of the aorta. We sought in this study to identify a set of CT-based geometric parameters that would better predict the risk of rupture than Dmax.
Methods: We obtained CT Scans from 180 patients (90 ruptured AAA, 90 elective AAA repair) and then used automated software to calculate 1-dimensional, 2-dimensional, and 3-dimensional geometric parameters for each AAA. Linear regression was used to identify univariate correlates of membership in the rupture group. We then used stepwise backward elimination to generate a logistic regression model for prediction of rupture.
Results: Linear regression identified 40 correlates of rupture. Following stepwise backward elimination, we developed a multi-variate logistic regression model containing 15 geometric parameters, including Dmax. This model was compared to a model containing Dmax alone. The multivariate model correctly classified 98% of all cases, whereas the Dmax-only model correctly classified 72% of cases. Receiver operating characteristic (ROC) analysis showed that the multivariate model had an area-under-the-curve (AUC) of 0.995, as compared to 0.770 for the Dmax-only model. This difference was highly significant (P< 0.0001).
Conclusion: This study demonstrates that a multivariable model using geometric factors entirely measurable from CT scanning can be a better predictor of AAA rupture than maximum diameter alone.

Introduction

Abdominal aortic aneurysms (AAA) are an important preventable cause of death in patients over age 65. Currently, the rupture risk of AAA is determined based on measurement of the maximum aortic diameter [2]. The current evidence-based threshold for surgical repair of AAA is 5.5 cm. However, diameter is not always an accurate predictor of rupture risk. For example, some aneurysms over 5.5 cm do not rupture, whereas a significant fractions of aneurysms that do rupture have a diameter smaller than 5.5 cm [2,3]. Therefore, refinement in the ability to predict AAA rupture would improve patient selection for AAA interventional treatment. In turn, this could result in improved patient outcomes and better resource utilization.
The purpose of this investigation was to use computed tomography (CT) scan imaging data to find if there exists a more accurate metric to predict aneurysm rupture than the standard of care maximum diameter. Our focus was to use geometric parameters as potential predictors of AAA rupture. We used image analysis to measure several 1-dimensional, 2-dimensional, and 3-dimensional geometric factors which describe the AAA and associated intraluminal thrombus. Our hypothesis was that a model including multiple geometry-based parameters would be superior to using maximum diameter alone as a predictor of AAA rupture. This hypothesis is supported by previously published work on AAA geometry quantification [2,4,5].

Methods

This study was conducted with approval from the Institutional Review Boards of both Allegheny General Hospital (Pittsburgh, PA) and Northwestern Memorial Hospital (Chicago, IL). We obtained contrast-enhanced CT scans from the retrospective review of the medical records of 180 patients, 90 of whom were either symptomatic or had a confirmed ruptured AAA, and 90 who were asymptomatic and had elective AAA repair. The images were processed using AAA Vasc 1.0, in-house image analysis application developed at Carnegie Mellon University to calculate the geometric parameters for each AAA. This process, which was described previously [5-7] involved: (1) image segmentation, including detection of the lumen, inner and outer wall boundaries of the AAA, (2) 3-dimensional reconstruction and meshing, and (3) computation of the geometric parameters that describe the size, shape, curvature, and regional variations of wall thickness.
Sixty geometric parameters were calculated for each AAA, as shown in Table 1. These included 11 one-dimensional indices, 9 two-dimensional indices, 4 three-dimensional size indices, 1 threedimensional shape index, 5 thrombus-related indices, 18 secondorder curvature-based indices, and 12 wall-thickness indices. All length metrics were measured in millimeters (mm). Measurement of the geometric parameters depends heavily on identifying the wall of the aorta, both in non-ruptured and in ruptured AAA cases. The algorithm to identify the aortic all has been described and validated in previous publications [5-7].
A linear regression analysis was performed to determine whether each geometric parameter had a significant correlation (either positive or negative) with membership in the rupture group, based on the use of Med Calc (v16.8, Ostend, Belgium). Subsequently, a predictive logistic regression model was developed in R (The R Foundation) by using the significant parameters (based on a statistical significance level of P< 0.05) in a stepwise backward elimination method [8]. The ensuing variables identified were then used to compare the multivariate model’s predictive ability against that of the maximum diameter alone, using Med Calc.

Table 1

×

Geometric Parameter	Description	Univariate correlate	Logistic regression model
1D Size Indices
Dmax	Maximum transverse diameter for all cross sections within the AAA sac	YES	YES
Dneck,p	Proximal neck diameter immediately below the renal arteries	YES	-
Dneck,d	Distal neck diameter	-	-
H	Height of AAA	YES	-
L	Centerline length of AAA	YES	-
Hneck	Height of AAA neck	-	-
Lneck	Centerline length of AAA neck	-	-
Hsac	Height of AAA sac	YES	YES
Lsac	Centerline length of AAA sac	YES	YES
Hb	Bulge height (distance from top of AAA to level where Dmax occurs)	-
dc	Distance between the lumen centroid and the centroid of the cross section where Dmax is located	YES	YES
2D Shape Indices
DHr	Diameter-Height ratio, Dmax/H (an expression of the fusiform shape of the AAA sac)	YES	YES
DDr	Diameter-Diameter ratio, Dmax/Dneck,p	YES	-
Hr	Height ratio, Hneck­/H (an assessment of the relative neck height in comparison with the AAA height)	-	-
BL	Bulge Location, Hb/H (a measure of the relative position of the maximum transverse dimension)	-	-
β	Asymmetry factor, 1 - (dc/Dmax)	-	-
T	Tortuosity, L/d, where d is the Euclidean (centerline) distance from the centroid of the cross section where Dneck,p is located to the centroid of the cross section at the AAA distal end	YES	-
Cave	average lumen compactness [Compactness, perimeter2/4πArea was calculated for each slice. Note that a circle has a minimum compactness value of 1]	-	-
Cmin	minimum lumen compactness	YES	-
Cmax	maximum lumen compactness	YES	-
3D Size Indices
V	Vessel volume	YES	-
S	Vessel surface area	-	-
VILT	Volume of intraluminal thrombus (ILT) contained within AAA sac	YES	-
γ	Ratio of AAA ILT volume, VILT/V	YES	YES
3D Shape Index
IPR	isoperimetric ratio S/V2/3[Measure of 3-D compactness of the whole aneurysm (minimum surface area that encompasses the maximum volume)]	-	-
Thrombus Content Indices
tt,ave	average thrombus thickness	YES	YES
tt, max	maximum thrombus thickness	YES	-
tt, min	minimum thrombus thickness	-	-
tt, minLoc	location of the minimum thickness	-	-
tt, maxLoc	location of the maximum thickness	-	-
Second Order Curvature Based Indices
GAA	Area averaged Gaussian curvature	YES	-
MAA	Area averaged Mean curvature	YES	-
GLN	L2 norm of the Gaussian curvature (Measure of irregularity on surface of aneurysm)	YES	-
MLN	L2 norm of the Mean curvature (Measure of irregularity on surface of aneurysm)	YES	-
Kmin	minimum Gaussian curvature	YES	YES
Kmax	maximum Gaussian curvature	YES	-
Kave	average Gaussian curvature	YES	-
Kmedian	median Gaussian curvature	-	-
Kmode	mode of the Gaussian curvature	-	-
Kvar	variance of the Gaussian curvature	YES	-
Mmin	minimum Mean curvature	YES	YES
Mmax	maximum Mean curvature	YES	-
Mave	average Mean curvature	YES	YES
Mmedian	median of the Mean curvature	YES	YES
Mmode	mode of the Mean curvature	YES	-
Mvar	variance of the Mean curvature	YES	-
Kskew	skewness of the Gaussian curvature; indicates whether the distribution of Gaussian curvature is normal, positive skew, or negative skew (Expressed as a percentage of the total Gaussian curvatures that falls above the average)	YES	-
Mskew	skewness of the Mean curvature; indicates whether the distribution of Mean curvature is normal, positive skew, or negative skew (Expressed as a percentage of the total Mean curvatures that falls above the average)	YES	-
Wall Thickness Indices
tw,min	minimum wall thickness	YES	YES
tw,max	maximum wall thickness	-	-
tw,ave	average wall thickness	-	-
tw,Dmax	average wall thickness where Dmax is located	YES	-
tw,mode	mode of the wall thickness	YES	-
tw,median	median of the wall thickness	-	-
tw,minVar	minimum variance of the wall thickness	-	-
tw,maxVar	maximum variance of the wall thickness	YES	YES
tw,medianVar	median variance of the wall thickness	YES	-
tw,modeVar	mode variance of the wall thickness	-	-
tw,meanVar	mean variance of the wall thickness	YES	YES
tw,skew	skewness of wall thickness distribution; indicates whether the distribution of wall thickness is normal, positive skew, or negative skew (Expressed as a percentage of the total thickness values that fall above the average)	YES	YES

Table 1: Description of the 60 geometric parameters evaluated by means of image-based quantitative geometric characterization, the binary outcome of the univariate linear regression analysis, which yielded 40 parameters correlated with AAA rupture, and the binary outcome of the logistic regression model, which yielded 15 of the correlates as statistically significant for the predictive model.

Table 1
Description of the 60 geometric parameters evaluated by means of image-based quantitative geometric characterization, the binary outcome of the univariate linear regression analysis, which yielded 40 parameters correlated with AAA rupture, and the binary outcome of the logistic regression model, which yielded 15 of the correlates as statistically significant for the predictive model.

Table 2

×

Geometric Parameter	Coefficient	Standard Error	P-value
Dmax	0.27113	0.12000	0.0239
Hsac	-0.55326	0.18827	0.0033
Lsac	0.39616	0.13728	0.0039
dc	-0.82677	0.28007	0.0032
DHr	-40.57045	13.44428	0.0025
γ	-3.21309	3.68288	0.3830
tt,ave	0.93756	0.29208	0.0013
Kmin	0.39480	0.16742	0.0184
Mmin	-0.17775	0.069802	0.0109
Mave	-105.09155	36.61836	0.0041
Mmedian	142.57814	47.60527	0.0027
tw,min	5.10129	2.60689	0.0504
tw,maxVar	-6.85256	2.60802	0.0086
tw,meanVar	27.99280	9.96467	0.0050
tw,skew	-0.14136	0.081303	0.0821
Constant	27.38134	15.66098	0.0804

Table 2: Coefficients, standard errors and P-values for the 15 significant geometric correlates of the multivariate logistic regression model.

Table 2
Coefficients, standard errors and P-values for the 15 significant geometric correlates of the multivariate logistic regression model.

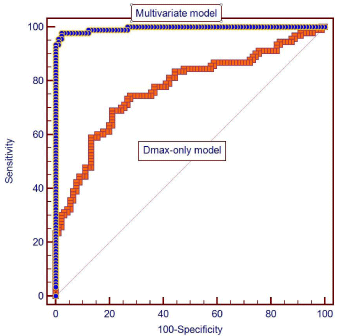
Figure 1

×Close

This text will be overwritten by jQuery

Figure 1
Receiver operating characteristic (ROC) curves for multivariate and maximum diameter-only models. The area-under-the-curve is significantly larger for the multivariate model indicating higher sensitivity and specificity of the model for identifying an aneurysm as ruptured.

Table 3

×

Geometric Parameter	Coefficient	Standard Error	P-value
Dmax	0.072099	0.013267	< 0.0001
Constant	-4.41201	0.81242	< 0.0001

Table 3: Coefficients, standard errors and P-values for aunivariate logistic regression model that includes maximum diameter as the only geometric correlate.

Table 3
Coefficients, standard errors and P-values for aunivariate logistic regression model that includes maximum diameter as the only geometric correlate.

Table 4

×

Actual Groups	Predicted Groups		Percent correct
	Elective Repair (probability < 0.5)	Ruptured (probability ≥0.5)
Elective Repair	88	2	97.8%
Ruptured	2	88	97.8%
Percent of cases correctly classified:			97.8%

Table 4: Summary of classification results for multivariate logistic regression model (with 15 geometric correlates) considering membership in elective repair or ruptured groups.

Table 4
Summary of classification results for multivariate logistic regression model (with 15 geometric correlates) considering membership in elective repair or ruptured groups.

Table 5

×

>

Actual Groups	Predicted Groups		Percent correct
	Elective Repair (probability < 0.5; Dmax < 61.2 mm)	Ruptured (probability ≥0.5; Dmax ≥61.2 mm)
Elective Repair	71	19	78.9%
Ruptured	31	59	65.6%
Percent of cases correctly classified:			72.2%

Table 5: Summary of classification results for univariate logistic regression model (with maximum diameter as the only correlate) considering membership in elective repair or ruptured groups.

Table 5
Summary of classification results for univariate logistic regression model (with maximum diameter as the only correlate) considering membership in elective repair or ruptured groups.

Results

As shown in Table 1, univariate linear regression, using membership in the rupture group as the dependent variable, identified 40 geometric parameters as significant correlates of rupture. The latter were entered into a multivariate logistic regression model and fifteen of the correlates were identified in this manner as being statistically significant for the predictive model. Table 2 describes the logistic regression coefficients for each parameter, the standard error, and the P-value for each coefficient and for the constant in this logistic regression equation. The model includes 4 one-dimensional indices, 1 two-dimensional index, 1 three-dimensional size index, 1 thrombus-related index, 4 second-order curvature-based indices, and 4 wall-thickness indices.
For comparison, we used the same data set to create a univariate logistic regression model using only maximum diameter (Dmax) as the independent predictor. Table 3 shows the coefficient, the standard error, and the P-value for Dmax and for the constant in this logistic regression equation. In this model, the predicted probability of rupture is greater than 50% when Dmax exceeds 61.2 mm.
The two predictive models were subsequently compared as follows. Patients were predicted to belong to either the elective repair or ruptured groups on the basis of the calculated probability being < 50% or ≥50%. This predicted classification was compared to the actual patient classification. Table 4 shows that the multivariate model correctly classified 98% of the study patients. By contrast, the Dmax-only model classified 72% of the patients, as shown in Table 5. Receiver operating characteristic (ROC) curves were constructed for each model. As illustrated in Figure 1, the ROC curve for the multivariate model had higher sensitivity and specificity for predicting membership in the rupture group than the ROC curve of the Dmax- only model. The area under the curve (AUC) for the multivariate model was 0.995, while the AUC for the Dmax-only model was 0.770. This difference was statistically significant (P< 0.0001).

Discussion

AAA maximum diameter is widely used clinically to assess the probability of aneurysm rupture. However, recent image-based modeling research suggests that the risk of rupture can be better predicted using other metrics. These include wall stress [9-17], wall shear stress [18], geometric factors other than diameter [2,4], and thrombus-related factors [19,20].
The present work focused on the hypothesis that geometric characteristics of the AAA sac and the associated thrombus could be used to predict rupture. The analysis was limited to parameters that can be measured from standard of care CT images. The methodology used semi-automatic CT scan segmentation and meshing to measure detailed geometric parameters of 180 patients with AAA. Of these, 90 received elective repair due to the maximum diameter of their aneurysm meeting or exceeding the critical value clinically recommended for repair and 90 presented with rupture or were symptomatic and received emergent repair within 1 month of the CT scan used for this study. We found that a model using multiple geometric parameters was far superior at classifying patients in the ruptured or elective repair groups, compared to a model relying on maximum diameter alone. Noteworthy is that our multivariate model also includes maximum diameter as an important predictive factor.
A predictive model based on geometric parameters derived from standard of care CT images is theoretically easier to implement clinically than a model requiring biomechanical parameters such as wall stress and shear stress. The rationale for this is that the accurate calculation of stress requires the implementation of finite element analysis or computational fluid dynamics modeling, and knowledge of non-anatomic factors such as individual blood pressure and heart rate at the time of administration of the CT scan. The geometric parameters used in the current study require specialized software analysis, but they can all be measured from the CT scan alone.
The multivariate regression model we identified in this study correctly classified 98% of the patients we used to create the model, whereas the Dmax-only regression model correctly classified only 72% of patients. This does not necessarily mean that the multivariate model will correctly classify new AAA patients with the same level of accuracy, specificity or sensitivity. Additional studies with larger population groups will be necessary to determine the clinical utility of the model. However, our findings suggest that rupture can be better predicted using a multivariate model compared to measuring maximum diameter only. This has important implications for monitoring of AAA patients and selection of cases for surgery.
The fact that a multivariate model is a better classifier of patients indicates that the additional geometric parameters besides Dmax have an important role in determining whether an aneurysm ruptures. This concept is consistent with several recent publications [2,4,9-12,15- 20]. Wall stress, AAA growth and rupture have all been shown to be dependent on factors other than aneurysm diameter. The precise biomechanical significance of the factors identified in the current study remains to be clarified. Additional analysis will be needed to determine, for example, whether these factors are associated with changes in wall stress or material fatigue.
This investigation has important limitations. First, some of the aneurysms in the elective repair group may have been close to rupture had they not undergone elective surgical repair. There is no way to know what might have happened to these otherwise asymptomatic patients. Furthermore, most of the patients in our ruptured cohort had already suffered rupture, an event that may substantively change the AAA geometry compared with their state immediately before rupture. This limitation is inherent in the study of this particular subject, because it would be unethical to deny patients surgical intervention for the purpose of monitoring them until they suffer rupture. Additionally, stepwise backward elimination was used to derive the multivariate model in this study but there are many other methods that could have been used; potentially, other strategies such as those based on machine learning techniques [4,21,22] may have yielded a better model.

Conclusion

This study demonstrates that a multi-variable regression model using 15 geometric parameters measurable from standard of care computed tomography angiography images can be a better predictor of AAA rupture than maximum diameter alone.

Funding

Research funding from the Bill and Melinda Gates Foundation, Carnegie Mellon University’s Biomedical Engineering Department, the John and Claire Bertucci Graduate Fellowship program, and NIH grants R21EB007651, R21EB008804, and R15HL087268.

Acknowledgement

The authors gratefully acknowledge the valuable help of Mark Eskandari, MD for contributing the CT images from Northwestern University and Satish Muluk, MD for contributing the CT images from Allegheny General Hospital.

References

1. Jeong JH, Kim JT, Kim NS, Cho JH, Kim JH, Oh JY, et al. Riskdiagnosis based on diameter of abdominal aortic aneurysm. Technol Health Care. 2016; 24: S569-S575.
2. Raut SS, Chandra S, Shum J, Washington CB, Muluk SC, Rodriguez JF, et al. Biological. Geometric and biomechanical factors influencing abdominal aortic aneurysm rupture risk: A comprehensive review. Recent Patents Med Imaging. 2013; 3: 44-59.
3. Darling RC, Messina CR, Brewster DC, Ottinger LW. Autopsystudy of unoperated abdominal aortic-aneurysms - Case for early resection. Circulation. 1977; 56: 161-164.
4. Lee K, Zhu J, Shum J, Zhang Y, Muluk SC, Chandra A, et al. Surface curvature as a classifier of abdominal aortic aneurysms: a comparative analysis. Ann Biomed Eng. 2013; 41: 562-576.
5. Shum J, Martufi G, Di Martino E, Washington CB, Grisafi J, Muluk SC, et al. Quantitative assessment of abdominal aortic aneurysm geometry. Ann Biomed Eng. 2010; 39: 277-286.
6. Shum J, Di Martino ES, Goldhammer A, Goldman D, Acker L, Patel G, et al. Semiautomatic vessel wall detection and quantification of wall thickness in computed tomography images of human abdominal aortic aneurysms. Med Phys. 2010; 37: 638-648.
7. Shum J, Xu A, Chatnuntawech I, Finol EA. A framework for the automatic generation of surface topologies for abdominal aortic aneurysm models. Ann Biomed Eng. 2011; 39: 249-259.
8. R Core Team. R: A Language and Environment for Statistical Computing. 2013.
9. Di Martino ES, Bohra A, Vande Geest JP, Gupta N, Makaroun MS, Vorp DA. Biomechanical properties of ruptured versus electively repaired abdominal aortic aneurysm wall tissue. J Vasc Surg. 2006; 43: 570-576.
10. Di Martino ES, Guadagni G, Fumero A, Ballerini G, Spirito R, Biglioli P, et al. Fluid-structure interaction within realistic three-dimensional models of the aneurysmatic aorta as a guidance to assess the risk of rupture of the aneurysm. Med Eng Phys. 2001; 23: 647-655.
11. Fillinger MF, Marra SP, Raghavan ML, Kennedy FE. Prediction of rupture risk in abdominal aortic aneurysm during observation: Wall stress versus diameter. J Vasc Surg. 2003; 37: 724-732.
12. Fillinger MF, Racusin J, Baker RK, Cronenwett JL, Teutelink A, SchermerhornML, et al. Anatomic characteristics of ruptured abdominal aortic aneurysm on conventional CT scans: Implications for rupture risk. J Vasc Surg. 2004; 39: 1243-1252.
13. Kleinstreuer C, Li Z. Analysis and computer program for rupture-risk prediction of abdominal aortic aneurysms. Biomed Eng Online. 2006; 5: 19.
14. Larsson E, Labruto F, Gasser TC, Swedenborg J, Hultgren R. Analysis of aortic wall stress and rupture risk in patients with abdominal aortic aneurysm with a gender perspective. J Vasc Surg. 2011; 54: 295-299.
15. Erhart P, Hyhlik-Dürr A, Geisbüsch P, Kotelis D, Müller-Eschner M, Gasser TC, et al. Finite element analysis in asymptomatic,symptomatic, and ruptured abdominal aortic aneurysms: in search of new rupturerisk predictors. Eur J Vasc Endovasc Surg. 2015; 49: 239-245.
16. Khosla S, Morris DR, Moxon JV, Walker PJ, Gasser TC, Golledge J. Metaanalysis of peak wall stress in ruptured, symptomatic and intact abdominal aortic aneurysms. Br J Surg. 2014; 101: 1350-1357.
17. Lindquist Liljeqvist M, Hultgren R, Gasser TC, Roy J. Volume growth of abdominal aortic aneurysms correlates with baseline volume and increasing finite element analysis-derived rupture risk. J Vasc Surg. 2016; 63: 1434-1442.
18. Boyd AJ, Kuhn DCS, Lozowy RJ, Kulbisky GP. Low wall shear stress predominates at sites of abdominal aortic aneurysm rupture. J Vasc Surg. 2015; 63: 1-7.
19. Thubrikar MJ, Robicsek F, Labrosse M, Chervenkoff V, Fowler BL. Effect of thrombus on abdominal aortic aneurysm wall dilation and stress. J Cardiovasc Surg. 2003; 44: 67-77.
20. Vorp DA, Lee PC, Wang DHJ, Makaroun MS, Nemoto EM, Ogawa S, et al. Association of intraluminal thrombus in abdominal aortic aneurysm with local hypoxia and wall weakening. J Vasc Surg. 2001; 34: 291-299.
21. Monsalve-Torra A, Ruiz-Fernandez D, Marin-Alonso O, Soriano-Payá A, Camacho-Mackenzie J, Carreño-Jaimes M. Using machine learning methods forpredicting inhospital mortality in patients undergoing open repair of abdominalaortic aneurysm. J Biomed Inform. 2016; 62: 195-201.
22. Canchi T, Kumar SD, Ng EY, Narayanan S. A review of computational methods topredict the risk of rupture of abdominal aortic aneurysms. Biomed Res Int. 2015; 2015: 861627.